5.1.1 DE DRAAGKRACHT
De draagkracht van het zweefvliegtuig wordt bijna helemaal door de vleugels geleverd. Naast de vleugels levert ook het stabilo een bijdrage. De grootte van de draagkracht is afhankelijk van volgende vijf factoren:
| 1. de luchtsnelheid | (V) | |
| 2. de grootte van het vleugeloppervlak | (S) | |
|
3. de aanvalshoek van de vleugel 4. de eigenschappen van de vleugelprofielvorm |
(α) | }Cl |
| 5. de luchtdichtheid | (ρ) |
1. DE LUCHTSNELHEID
Een snelheidsmeter in een auto meet de grondsnelheid, de snelheid waarmee je over de weg rijdt. Een snelheidsmeter in een vliegtuig meet de snelheid van de langsstromende lucht. Dit is de luchtsnelheid en dus niet de grondsnelheid. Wanneer je twee keer zo snel vliegt dan is de draagkracht vier keer zo groot. De draagkracht is recht evenredig met het kwadraat van de vliegsnelheid en recht evenredig met de luchtdichtheid ρ.
2. DE GROOTTE VAN HET VLEUGELOPPERVLAK
Een LS4 heeft een vleugeloppervlak van 10,5 m2 en een DG1000 in de 20 meter versie heeft een vleugeloppervlak van 17,6 m2. Zwaardere vliegtuigen hebben een groter vleugeloppervlak nodig. Twee keer zo'n groot oppervlak levert bij dezelfde snelheid en zelfde aanvalshoek twee keer zoveel draagkracht. De draagkracht is dus recht evenredig met het vleugeloppervlak.
Een LS4 heeft een vleugeloppervlak van ongeveer 10 m2. Een LS4 weegt met een piloot van 80 kg ongeveer 350 kg. Elke vierkante meter vleugeloppervlak levert dan ongeveer 35 kg draagkracht. Het gewicht gedeeld door het vleugeloppervlak noemen we de vleugelbelasting. Die is in dit voorbeeld 35 kg. Bij een lichtere piloot wordt de vleugelbelasting lager en door met water te vliegen wordt de vleugelbelasting groter.
3. DE AANVALSHOEK VAN DE VLEUGEL
De Engelsen spreken over de ‘angle of attack’, de Belgen over de ‘aanvalshoek’ en de Nederlanders noemen de hoek die de aanstromende lucht met de koorde van de vleugel maakt, de invalshoek. In de tekening is α de aanvalshoek. 
Hoe groter de aanvalshoek hoe groter de draagkracht. Bij kleine aanvalshoeken neemt de draagkracht recht evenredig toe met de aanvalshoek. Twee keer zo'n grote aanvalshoek levert ongeveer twee keer zoveel draagkracht op. 

Bij een aanvalshoek van ongeveer 15° kan de luchtstroming het profiel van de vleugel niet meer volgen. De luchtstroming breekt af in wervels, eerst achteraan en schuift op naar voor. De lift (draagkracht) neemt behoorlijk af en de weerstand neemt behoorlijk toe.

Het loslaten van de luchtstroom noemen we overtrekken. Wanneer we aan de stuurknuppel trekken, dan trekken we de neus omhoog. We vergroten daardoor de aanvalshoek met de aanstromende lucht. Hierdoor zal het vliegtuig klimmen en/of vertragen. Vergroot je de aanvalshoek te veel, te veel trekken aan de stuurknuppel, dan overtrek je het vliegtuig.
DE AANVALSHOEK EN HET GEWICHT
De grootte van de lift is in hoge mate afhankelijk van de vliegsnelheid en van de aanvalshoek. Bij normale vliegsnelheid met twee inzittenden vlieg je met een aanvalshoek van ongeveer 7°. Je vliegt dan met een gunstige verhouding van lift en weerstand. Wat gebeurt er met de aanvalshoek als er twee lichtere piloten in zitten of als je solo vliegt in deze tweezitter en je vliegt wel met dezelfde vliegsnelheid? Het toestel is dan lichter geworden. Door het lagere gewicht kan de aanvalshoek lager zijn bij dezelfde vliegsnelheid en zo ontstaat er weer een evenwicht tussen de lift en het gewicht.
Stel je vliegt met iemand in een tweezitter met gewone snelheid en je gaat iets langzamer vliegen. Wat gebeurt er nu met de aanvalshoek? De snelheid wordt minder, dat betekent dat de snelheid een kleinere bijdrage aan de lift levert. Dan moet je de aanvalshoek groter maken (iets trekken aan de stuurknuppel) om meer lift te krijgen en weer evenwicht te maken met het gewicht. Of omgekeerd, wanneer je trekt aan de stuurknuppel zorgt de grotere aanvalshoek voor een grotere bijdrage aan de lift waardoor het vliegtuig trager zal vliegen om in evenwicht te blijven.

4. DE EIGENSCHAPPEN VAN DE PROFIELVORM (CL)
De CL zegt iets over de vorm van de vleugel en de stand van de vleugel in de luchtstroom (aanvalshoek). Wanneer je het vleugelprofiel van een ASK21 vergelijkt met een topklasse wedstrijdzwever dan zie je dat de vleugelprofielen erg verschillen. De ASK21 heeft een vrij dikke vleugel en een wedstrijdzwever een veel dunnere vleugel en de grootste dikte van de vleugel bevindt zich bij een topklasse zweefvliegtuig verder naar achteren. Bij zo'n vleugel blijft de stroming langer laminair. Laminaire stroming wordt uitgelegd bij 5.1.3 De weerstand

We verdelen de profielen in symmetrische en asymmetrische profielen. Het hoogteroer en het richtingsroer zijn symmetrisch. De vleugelprofielen zijn asymmetrisch. Je ziet hierboven dat de asymmetrische profielen verschillende vormen kunnen hebben. Elk vleugelprofiel heeft voor een bepaald doel de meest gunstige eigenschappen.
Koorde De langst mogelijke rechte lijn van de achterrand naar de vleugelneus is de koorde. Bij een symmetrisch profiel gaat die koorde precies door het midden. Zie de afbeelding hierboven. Op de tekening hieronder is naast de koorde ook de skeletlijn getekend. Dit is de lijn die het midden aangeeft van de profiel boven- en de profiel onderkant. De grootste afstand tussen de koorde en de skeletlijn geeft de profielwelving aan.

De profielvorm is van invloed op de drukverdeling aan de boven- en onderzijde van het vliegtuig.

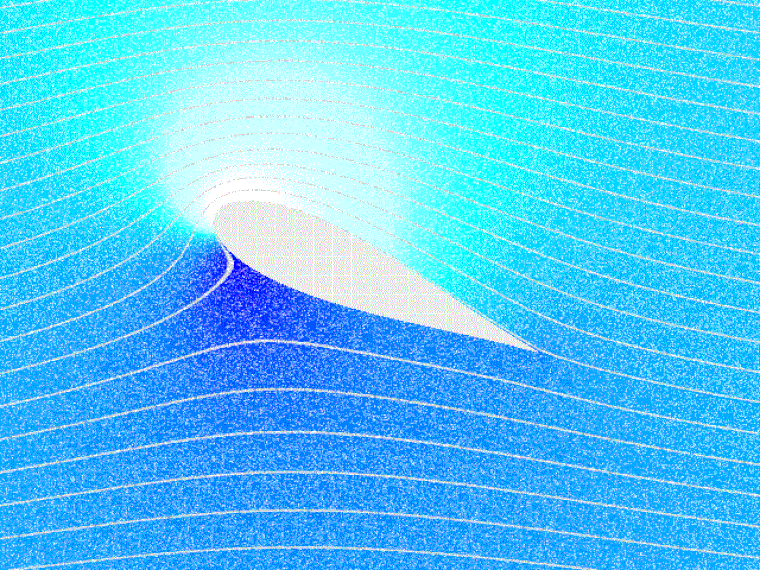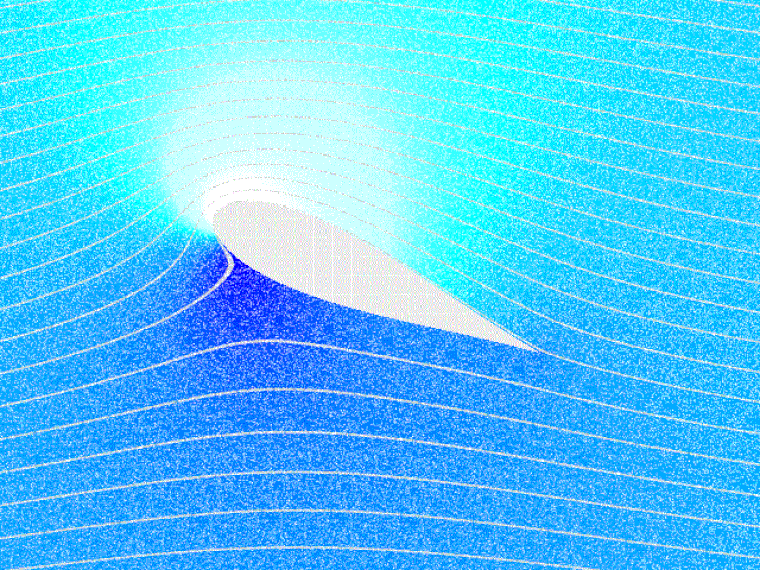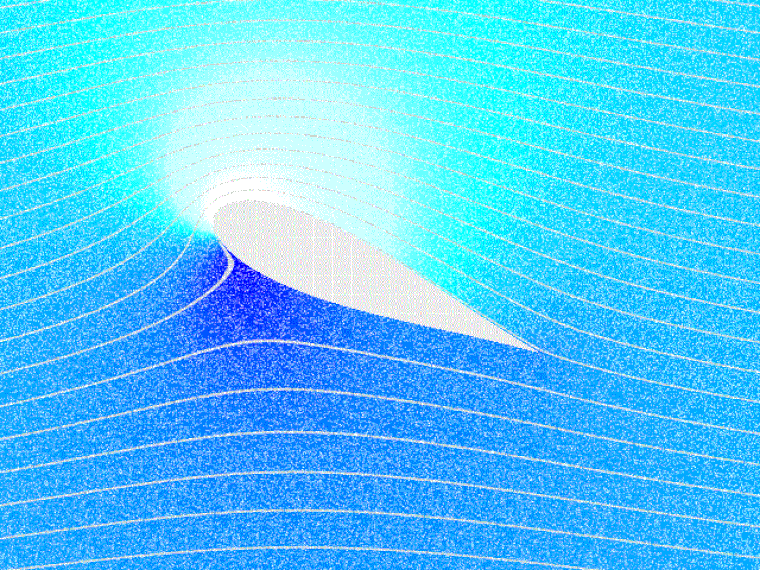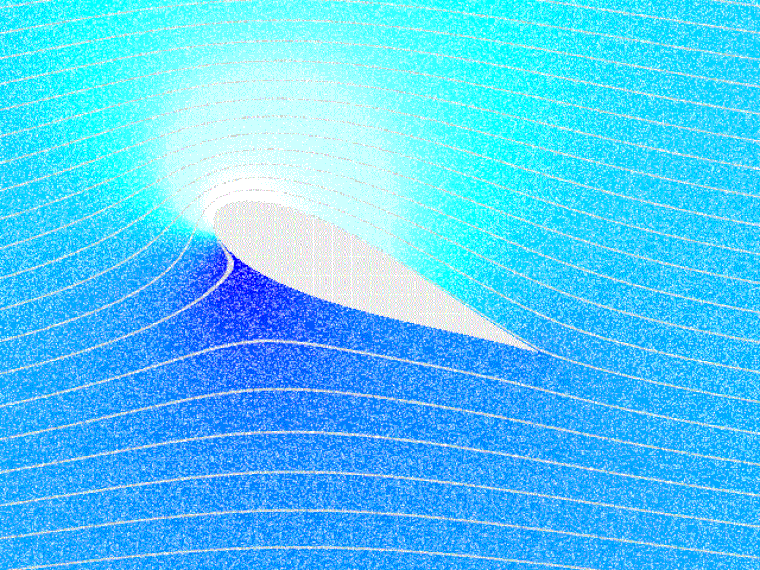

De overdruk aan de onderzijde van de vleugel en de onderdruk aan de bovenzijde van de vleugel zorgen voor de lift (draagkracht). Aan de lengte van de pijlen kun je zien dat de onderdruk aan de bovenzijde van de vleugel een veel grotere bijdrage (ongeveer 2/3) levert aan de lift dan de overdruk aan de onderzijde (ongeveer 1/3). De drukverdeling, zoals hier getekend, ziet er bij elke aanvalshoek anders uit. Algemeen kunnen we wel stellen dat (bij een klassiek vleugelprofiel en een aanvalshoek kleiner dan de kritische) de drukverdeling het grootst is aan de voorzijde van de vleugels. Het drukpunt is de plaats waar de luchtkrachten (lift en drag) in geconcentreerde vorm en de aerodynamische constante aangrijpen, te vergelijken met het zwaartepunt voor de zwaartekracht. Wanneer de aanvalshoek kleiner wordt, verschuift het drukpunt naar achteren. De D die bij de rode pijl staat, geeft de drag (de weerstand) weer. Bij symmetrische profielen verschuift het drukpunt niet met de aanvalshoek.

Op deze afbeelding zie je de aanvalshoek en het punt waar de lift het grootst is. Dit is een asymmetrisch profiel. Bij een aanvalshoek van 0° en ook bij -20 levert dit profiel wel enige lift. Hoe groter de aanvalshoek, hoe groter de lift en bovendien komt het punt waar de lift het grootst is, steeds meer naar voren te liggen.

Op de afbeelding zie je dat de hele vleugel bijdraagt aan de liftgeneratie, maar de drukverdeling is bij een grotere aanvalshoek anders dan bij een kleine aanvalshoek. Als de aanvalshoek groter wordt, gaat het drukpunt naar voren, want er ontstaat een toenemende onderdruk boven de neus van het profiel.
Door de verplaatsing van het drukpunt (en de verandering van grootte en richting) van de luchtkrachten verandert ook het moment. Stel dat op de afbeelding links het zwaartepunt precies tegenover de lift ligt, dan verschuift het drukpunt op de rechter afbeelding naar voren. Het zwaartepunt verschuift niet. Er is dan een moment om het zwaartepunt die de aanvalshoek verder wil vergroten. Ook het stabilo krijgt een grotere aanvalshoek en die herstelt de evenwichtssituatie weer.
Op de afbeelding hieronder zie je bij 1 een zweefvliegtuig vlak voor hij de thermiekbel binnen vliegt. Bij 2 vliegt hij net in de thermiekbel. Welke verschillen zie je?
Uit de praktijk weet je dat wanneer je een thermiekbel binnenvliegt, er twee dingen gebeuren. Je voelt het stijgen in je zitvlak en je moet iets aan de stuurknuppel trekken anders loopt de snelheid op. Bij het binnenvliegen van een thermiekbel wordt de aanvalshoek door een veranderde aanstroming groter. De draagkracht neemt toe en gaat iets voorover hellen, de stijgsnelheid neemt toe en de vliegsnelheid neemt toe. Dit voel je en je moet iets aan de stuurknuppel trekken om de juiste thermieksnelheid aan te houden. Bij het verlaten van de bel gebeurt het omgekeerde en moet je de stuurknuppel weer iets laten vieren.
Wanneer je te langzaam een sterke thermiekbel binnenvliegt, dan overtrekt het vliegtuig. Ondervindt één vleugel meer thermiek en de ander juist minder, bijvoorbeeld op de rand van de bel of door turbulentie, dan kan het vliegtuig in een tolvlucht vallen. Bij krachtige thermiek kun je daarom beter iets sneller vliegen. Met iets meer snelheid kun je in turbulente lucht het vliegtuig ook veel beter besturen.
ROERUITSLAG, REMKLEPPEN EN FLAPS
Vogels kunnen de vorm van hun vleugels veranderen. Dat doen ze bijvoorbeeld om bochten te maken of precies op een paal te landen. Zweefvliegtuigen hebben rolroeren, remkleppen en sommige toestellen hebben ook nog flaps. Daarmee kan het vleugelprofiel veranderd worden.
ROLROER
Een beweging van de stuurknuppel naar rechts geeft een rolroeruitslag aan de linkerkant omlaag en aan de rechterkant omhoog. Links wordt de aanvalshoek vergroot en wordt de luchtstroming meer naar beneden afgebogen. Daardoor ontstaat meer draagkant en meer weerstand aan de linkerkant. Rechts ontstaat door een uitslag van het rolroer omhoog minder draagkracht en minder weerstand.

REMKLEPPEN
Door het uittrekken van de remkleppen verhogen we de weerstand. Op de plaats waar de remkleppen verticaal op de vleugels omhoog gaan, laat de luchtstroming volledig los, neemt de weerstand behoorlijk toe en neemt de lift af. Vanwege hun grote effectiviteit worden remkleppen slechts over een klein gedeelte van de spanwijdte toegepast. Aangezien de overtreksnelheid met het gebruik van remkleppen iets toeneemt, gebruiken we de remkleppen alleen als we minimaal met landingssnelheid vliegen. Trek je de remkleppen, dan moet de verminderde draagkracht en grotere weerstand gecompenseerd worden door een grotere aanvalshoek, of door iets meer snelheid. Vaak zal je door de toegenomen weerstand de neus iets moeten drukken om de landingssnelheid vast te houden
FLAPS
Door het gebruik van flaps begint een vliegtuig meer op de vleugels van een vogel te lijken. Bij iedere snelheid past een optimale vorm van de vleugels. Met flaps kunnen we dit enigszins nabootsen. Een zweefvliegtuig met flaps (in het Nederlands welvingskleppen) kan de achterrand van de vleugel omhoog of omlaag doen. Omhoog heet negatief en omlaag positief.

Flaps negatief Bij hoge snelheden doe je de flaps omhoog. Je zet de flaps negatief, je maakt een gestrekt profiel. De lift neemt door een uitslag van de achterrand omhoog iets af maar de weerstand neemt ook af en dat is in die situatie gunstiger.
Flaps positief Bij thermieken en landen doe je de flaps naar beneden. Je zet de flaps positief, je maakt een gewelfd profiel. Je krijgt daardoor een grotere vleugelwelving, dus meer lift. De weerstand neemt iets toe maar dat is bij thermiekvliegen minder nadelig. De snelheid waarmee we thermiekvliegen is langzamer dan de steeksnelheden die we vliegen om van thermiekbel naar thermiekbel te vliegen. Het loont dus om met een positieve flapstand te thermieken en snel te vliegen met een negatieve flapstand.
Voor de landing hebben de flaps een aparte landingsstand. Naarmate de klep verder omlaag wordt uitgeslagen neemt de draagkracht (lift) en de weerstand toe. Hiervan kun je gebruik maken om de landing zo kort mogelijk te houden.
Op geringe hoogte brengt het gebruik van flaps gevaren met zich mee. Wanneer je de flaps uit de landingsstand haalt en bijvoorbeeld naar neutraal schuift, omdat je bijvoorbeeld ziet dat je anders voor je landingsveld landt, dan neemt de aanvalshoek af en kan het vliegtuig sterk 'doorzakken'. Daarom gebruik je in de landing de remkleppen en wanneer je ziet dat je je landingsveld zeker haalt, dan kun je de flaps in de landingsstand zetten en daar houd je ze dan ook in. De flaps uit de landingsstand halen, kan alleen met voldoende snelheid en hoogte.
5. DE LUCHTDICHTHEID
| Hoogte in meters | Luchtdruk hPa | Luchtdichtheid kg/m3 | Temperatuur in °C |
| 0 | 1013,3 | 1,225 | 15 |
| 1000 | 898,6 | 1,1116 | 8,5 |
| 2000 | 79,5 | 1,0065 | 2 |
| 3000 | 701,1 | 0,9091 | -4,5 |
| 5000 | 540,2 | 0,7361 | -17 |


Stellen we de beschikbare lift om het gewicht te dragen bij rechtuit vliegen op 100%, dan is er bij een helling van 30° nog 93% beschikbaar, bij 45° nog maar 70% en bij 60° nog maar 50%.
Vooral bij steilere bochten moeten we daar terdege rekening mee houden. De draagkracht (lift) neemt toe toe met het kwadraat van de snelheid (2 x zoveel snelheid is 4 x zoveel draagkracht). Bij het maken van bochten moeten we er rekening mee houden dat de overtreksnelheid met de toenemende dwarshelling ook toeneemt.
| Dwarshelling | Dwarshelling: Toename overtreksnelheid |
| 20° | ± 3% |
| 30° | ± 7% |
| 45° | ± 20% |
| 60° | ± 41% |
Bij bochten tot 30° hoef je de vliegsnelheid maar een beetje te verhogen. Bij steilere bochten verhoog je duidelijk de snelheid. Je doet dat door de snelheid vanuit de normale bocht te laten toenemen.



